৩৫ তম বিসিএস থেকে শুরু করে ৪৪ প্রতি বছর বিসিএস প্রিলিমিনারিতে অসমতা থেকে একটা প্রশ্ন আসে। মানবিক বা ব্যবসায় শাখার শিক্ষার্থীদের গনিত ভীতি থাকে। কিন্তু সহজেই অসমতার সমাধান শিখে বিসিএস প্রিলিমিনারির গনিতে ১ মার্ক নিশ্চিত করতে পারি।

আজকে আমরা সেটাই শিখার চেষ্টা করবো।

বিসিএস অসমতার সমাধান

৩৫ থেকে ৪৪ তম বিসিএসএ দুই ধরনের প্রশ্ন এসেছেঃ

ধরণ ১ঃ

অসমতার একপাশে x চলকের দ্বিঘাত সমীকরণ অন্যপাশে শুন্য দেওয়া থাকবে x এর সীমা নির্ণয় করতে হবে। যেমনঃ $$x^2 -5x +6 < 0$$​  এর সমাধান কোনটি? —–৩৭ তম বিসিএস

 $$2x^2 + 5x +3 > 0$$​  এর সমাধান কোনটি? —–৩৯ তম বিসিএস।

  $$x^2 - 3x -10 > 0$$​এর সমাধান কোনটি? —– ৪২ তম বিসিএস

 $$5x - x^2 -6 >0$$​এর সমাধান কোনটি? —– ৪৩ তম বিসিএস।

ধরণ ২ঃ

অসমতার একপাশে মডুলাস বা পরমমান সহকারে x চলকের একঘাত এবং অন্যপাশে ধ্রুবক সংখ্যা থাকে। যেমনঃ বাস্তব সংখ্যায় ।x-3| <5 এর সমাধান কোনটি? ——-৩৫ তম বিসিএস

বাস্তব সংখ্যায় ।2x-3| ≤1 এর সমাধান কোনটি?  ………৩৮ তম বিসিএস

বাস্তব সংখ্যায় ।x-2| <3  এর সমাধান কোনটি?  ………৪১ তম বিসিএস

বাস্তব সংখ্যায় ।3x+2| <7  এর সমাধান কোনটি?  ………৪৪ তম বিসিএস 

এছাড়া আরো একটি প্রশ্ন এসেছিলো ৪০ তম বিসিএস প্রিলিতেঃ 3x-2>2x-1 এর সমাধান সেট কোনটি?

সমাধান শুরু করার আগে কয়েকটা নিয়ম জেনে নেইঃ

১। অসমতার উভয় পক্ষকে (-১) বা ঋণাত্মক দিয়ে গুণ করলে অসমতার চিহ্ন পরিবর্তিত হয়। যেমনঃ -x>1, উভয়পক্ষকে -1 দিয়ে গুণ করলে -(-x) <-1 বা, x<-1.

২। উভয়পক্ষকে ইনভার্স করলে অর্থাৎ উভয়পাশের ভগ্নাংশকে উল্টালে অসমতার চিহ্ন পরিবর্তিত হয়। যেমনঃ 1/x<1/4 হলে x>4.

এবার আমরা সবচেয়ে সহজ ৪০ তম বিসিএসে আসা অসমতার প্রশ্নটি সমাধান করি 3x-2>2x-1 এর সমাধানঃ

ক) [1, ∞) খ) (1, ∞)

গ) [1/2, ∞) ঘ) [-1, ∞)

প্রথমে [1, ∞) ও (1, ∞) এর পার্থক্য জানা দরকার [1, ∞) এর অর্থ 1 এর সমান অথবা বড়, কিন্তু (1, ∞) এর অর্থ 1 থেকে বড় ।

এবার সমাধানে আসা যাকঃ 3x-2>2x-1 বা, 3x-2x>-1+2 বা, x>1 অর্থাৎ x, 1 অপেক্ষা বড়। অতেব খ নং উত্তর।

ধরণ ২ এর সমাধান করার চেষ্টা করিঃ

।x-3| <5 এর সমাধান কোনটি?

ক) 2<x<8 খ) -2<x<8

গ) -8<x<-2 ঘ) -4<x<-2

|x|<5 অর্থ x এর মান -5<x<5. সুতরাং ।x-3| <5 কে লিখা যায় -5<x-3<5

এখন আমাদের এমনভাবে যোগ-বিয়োগ গুন বা ভাগ করা লাগবে যেন মাঝে শুধু x থাকে। সমীকরণের প্রতি পাশে যদি 3 যোগ করি তাহলে মাঝে শুধু x থাকবে। তাই উভয় পাশে 3 যোগ করে পাই -5+3<x-3+3<5+3 বা, -2<x<8, অতএব খ নং উত্তর।

অনুরূপঃ ।2x-3| ≤1 এর সমাধান কোনটি?

ক) 1<x<2 খ) x≤1 অথবা x≥2

গ) 1≤x≤2 ঘ) -1<x<2

বা, -1≤2x-3≤1 উভয়পাশে 3 যোগ করে পাই, -1+3≤2x-3+3≤1+3 বা, 2≤2x≤4. উভয়পাশে 2 দিয়ে ভাগ করলে মাঝে শুধু x আসবে, অতএব 1≤x≤2.

এখন ।x-2| <3 ও ।3x+2| <7 এর সমাধান নিজেরাই বের করুন তারপর আমার সাথে মিলিয়ে নেনঃ প্রথমটির উত্তর হবে -1<x<5 ও দ্বিতীয়টির উত্তর হবে -3<x<5/3.

ধরণ ১ এর সমাধান শিখিঃ

$$x^2 -5x +6 < 0$$ এর সমাধান কোনটি? —–৩৭ তম বিসিএস

ক) 2<x<3 খ) -3<x<-2

গ) x<2 ঘ) x<3

এ জাতীয় অসমতার সমাধান করার করার জন্য প্রথমে দ্বিঘাত সমীকরণকে দুইটি উৎপাদকের গুণফল আকারে প্রকাশ করতে হবে। $$x^2 -5x +6 < 0$$ = $$x^2 -2x -3x +6$$​  = x(x-2) -3(x-2) = (x-2)(x-3)

অতএব, (x-2)(x-3) <0

এখনও কিন্তু সমাধান শেষ হয়নি। এখন আমরা দারুন একটা ট্রিক্স শিখবো, চলুন শুরু করা যাকঃ

উৎপাদকের সমাধানগুলো সংখ্যারেখার নিয়ম অনুযায়ী সরলরেখায় বসায়, এখানে সমাধানগুলো হলো 2 ও 3। সংখ্যারেখায় 2 ও 3 বসিয়ে পাইঃ

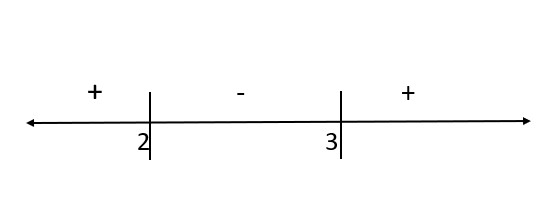
এবার সংখ্যারেখার যে অংশটুকু শর্তের সাথে মিলে সে অংশটুকু উত্তর। প্রশ্নে উৎপাদকের গুণফল <0, অর্থাৎ,(-)চিহ্নিত অংশটুকু উত্তর। সুতরাং উত্তর হবেঃ 2<x<3.

বলে রাখা ভালো, প্রশ্নে উৎপাদকের গুণফল >0 দেওয়া থাকলে (+) চিহ্নিত অংশটুকু উত্তর হতো, অর্থাৎ, উত্তর হতোঃ x>3 এবং x<2. 3 এর ডানপাশে (+) তাই x>3 হয়েছে। আবার 2 এর বামপাশের (+) অংশটুকু 2 অপেক্ষা ছোট হওয়ায় x<2 হয়েছে।

আরেকটা সমাধান করা যাকঃ

$$5x -x^2 -6 >0$$​  এর সমাধান কোনটি? —– ৪৩ তম বিসিএস।

ক) x>3, x<2 খ) 2>x>3

গ) x<2 ঘ) 2<x<3

$$5x -x^2 -6 >0$$ বা,   $$-5x + x^2 +6 < 0$$​   আগেই বলেছি অসমতার সমীকরণের উভয়পাশে (-) দিয়ে গুণ করলে অসমতার চিহ্ন পরিবর্তিত হয়। সুতরাং,   $$x^2-5x +6 < 0$$​   এখন প্রশ্নটা ঠিক আগের প্রশ্নের মত হয়ে গেছে খেয়াল করে দেখুন। অতএব, উত্তর হবে 2<x<3।

পরবর্তী প্রশ্নঃ 

 $$x^2 -3x -10 >0$$​   এর সমাধান কোনটি? —– ৪২ তম বিসিএস

ক) (-∞, -1) U (4, +∞) খ) (-∞, -2) U (5, +∞)

গ) (∞, 2) U (5, +∞) গ) (-5, -∞) U (∞, 2)

$$x^2 -3x -10 >0$$   বা,    $$x^2 -5x -10 >0$$​ বা, x(x-5)+2(x-5)>0 বা, (x-5)(x+2)>0 উৎপাদকগুলোর সমাধানঃ -2, 5. সংখ্যারেখায় -2 ও 5 বসিয়ে এবং একইভাবে +, – বসিয়ে পাইঃ

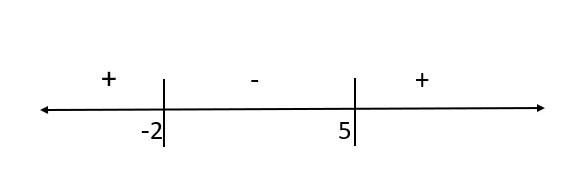
প্রশ্নের সমীকরনটি >0 হওয়ায় (+) চিহ্নিত অংশগুলো উত্তর হবে। অর্থাৎ, উত্তর x<-2 বা, x>5. যা -∞x<-2 বা 5<x<∞ এর সমান। উত্তর হবে (-∞, -2) U (5, +∞) ।